数学函数
数学函数
| 命名规则 | 多值函数 |
| 一般和非一般情况 | 数学常数 |
| 数值函数 | 正交多项式 |
| 分段函数 | 特殊函数 |
| 伪随机数 | 椭圆积分和椭圆函数 |
| 整数和数论中的函数 | Mathieu 函数和相关的函数 |
| 组合函数 | 带有特殊函数的运算 |
| 初等超越函数 |
Wolfram 语言中的数学函数根据定义规则来命名. 对大多数 Wolfram 语言函数,名称通常是完整的完全拼写的英语单词. 对于一些很常见的函数,Wolfram 语言使用传统缩写. 例如,模函数的名称是 Mod,而不是 Modulo.
通常涉及人的名字的数学函数在 Wolfram 语言中有形如 PersonSymbol 的名称. 例如,勒让德多项式 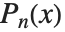 被表示为LegendreP[n,x]. 尽管这个惯例使函数的名称较长,但它避免了任何模棱两可或混乱不清.
被表示为LegendreP[n,x]. 尽管这个惯例使函数的名称较长,但它避免了任何模棱两可或混乱不清.
| IntegerPart[x] | x 的整数部分 |
| FractionalPart[x] | x 的分数部分 |
| Round[x] | 最接近 x 的整数 〈x〉 |
| Floor[x] | 小于等于 x 的最大整数 ⌊x⌋ |
| Ceiling[x] | 大于等于 x 的最小整数 ⌈x⌉ |
| Rationalize[x] | 近似于 x 的有理数 |
| Rationalize[x,dx] | 容差 dx 内的有理数近似 |
| x | IntegerPart[x] | FractionalPart[x] | Round[x] | Floor[x] | Ceiling[x] |
| 2.4 | 2 | 0.4 | 2 | 2 | 3 |
| 2.5 | 2 | 0.5 | 2 | 2 | 3 |
| 2.6 | 2 | 0.6 | 3 | 2 | 3 |
| -2.4 | -2 | -0.4 | -2 | -3 | -2 |
| -2.5 | -2 | -0.5 | -2 | -3 | -2 |
| -2.6 | -2 | -0.6 | -3 | -3 | -2 |
IntegerPart[x] 和 FractionalPart[x] 可以看作是提取小数点左边和右边的数字. Round[x] 常被用来强迫接近整数的一个数成为真正的整数. Floor[x] 和 Ceiling[x] 常出现在计算一个具有非整数间隔的数列中有多少元素的事项中.
| RealSign[x] | 对于 x>0 为 1;对于 x<0 为 -1 |
| UnitStep[x] | 对于 x≥0 为 1;对于 x<0 为 0 |
| RealAbs[x] | x 的绝对值 x |
| Clip[x] | 介于 ‐1 和 +1 之间的 x |
| Rescale[x,{xmin,xmax}] | 重新调整为从 0 到 1 的 x |
| Max[x1,x2,…] or Max[{x1,x2,…},…] | |
x1, x2, … 的最大值 | |
| Min[x1,x2,…] or Min[{x1,x2,…},…] | |
x1, x2, … 的最小值 | |
| x+I y | 复数 x+iy |
| Re[z] | 实部 Re z |
| Im[z] | 虚部 Im z |
| Conjugate[z] | 多共轭 z* 或 |
| Abs[z] | 绝对值 z |
| Arg[z] | 幅角 ϕ 使得 z=zei ϕ |
| Sign[z] | z≠0 时,复数 sign z/z |
经常地,在不同区域中具有不同形式的函数是很方便的. 这可以使用 Piecewise 来实现.
分段函数出现在在不同区域离散切换的系统中. 它们也是许多计算方法的核心,包括样条(splines)和有限元(finite elements). 特殊情况包括这样的函数如 Abs、UnitStep、Clip、Sign、Floor 和 Max. Wolfram 语言处理符号和数值两种情况下的分段函数.
| RandomInteger[] | 概率为 |
| RandomInteger[{imin,imax}] | 包含在 imin 和 imax 内的伪随机整数 |
| RandomInteger[imax] | 包含在 0 和 imax 内的伪随机整数 |
| RandomReal[ ] | 0 和 1 之间的伪随机实数 |
| RandomReal[{xmin, xmax}] | xmin 和 xmax 之间的伪随机实数 |
| RandomReal[xmax] | 0 和 xmax 之间的伪随机实数 |
| RandomComplex[] | 单位方域中的伪随机复数 |
| RandomComplex[{zmin,zmax}] | 由 zmin 和 zmax 定义的长方形中的伪随机复数 |
| RandomComplex[zmax] | 由 0 和 zmax 定义的长方形中的伪随机复数 |
| RandomReal[range,n]
,
RandomComplex[range,n]
,
RandomInteger[range,n] | |
从给定区域得到的 n 个伪随机数的列表 | |
| RandomReal[range,{n1,n2,…}]
,
RandomComplex[range,{n1,n2,…}]
,
RandomInteger[range,{n1,n2,…}] | |
由伪随机数组成的 n1×n2×… 数组 | |
选项名
|
默认值
| |
| WorkingPrecision | MachinePrecision | 用于实数或者复数的精度 |
使用伪随机数的一个常见方法是进行数值假设检验. 例如,如果用户相信两个符号表达式在数学上是相等的. 可以通过给符号参数插上“典型”数值的值. 然后比较数值结果来进行检验. (如果要这样做的话,在数值准确度问题上,在可能没有唯一值的复变量的函数上,都应当仔细注意).
用随机数字代入表明方程不总是为真 True:
RandomInteger、RandomReal 和 RandomComplex 与其他的 Wolfram 语言函数不同,每次调用它时,都将得到不同的结果. 因此,如果在计算中使用它们,在不同的时机会得到不同的答案.
由 RandomInteger、RandomReal 和 RandomComplex 得到的序列在多数意义下并不是“真正随机的”,尽管实际上它们应当是“足够随机的”. 事实上,这个序列是通过使用从一个特定起点开始的确定数学算法生成的. 如果给出相同的起点,将得到相同的序列.
如果用户想要确定总是得到相同的伪随机数序列,可以使用 SeedRandom 明显地给伪随机数生成一个起点.
| SeedRandom[] | 使用时钟时刻重设伪随机生成器的起点 |
| SeedRandom[s] | 使用整数 s 重设伪随机生成器的起点 |
每调用一次 RandomInteger、RandomReal 或者 RandomComplex,伪随机数生成器的内部状态就被改变,这意味着在辅助运算中调用这些函数,将会影响主运算中返回的数. 要避免这个问题,可以在运算 BlockRandom 中局部化这些函数的使用效果.
| BlockRandom[expr] | 使用局部化的伪随机生成器的当前状态计算 expr |
通过在 BlockRandom 中进行局部化计算,在生成第一个列表之后,伪随机数生成器的状态被恢复:
| RandomInteger[dist]
,
RandomReal[dist] | |
服从随机分布 dist 的伪随机数 | |
| RandomInteger[dist,n]
,
RandomReal[dist,n] | |
服从随机分布 dist 的 n 个伪随机数的列表 | |
| RandomInteger[dist,{n1,n2,…}]
,
RandomReal[dist,{n1,n2,…}] | |
由服从随机分布 dist 的伪随机数组成的 n1×n2×… 数组 | |
| RandomChoice[list, n] | 从 list 随机选择 n 个项 |
| RandomChoice[list,{n1,n2,…}] | 从 list 随机选择得到的值组成的 n1×n2×… 数组 |
| RandomSample[list, n] | 从 list 得到的大小为 n 的样本 |
| Mod[k,n] | k 模 n ( k 除以 n 的余数) |
| Quotient[m,n] | m 和 n 的商 ( m/n 的整数部分) |
| QuotientRemainder[m,n] | 商和余数的列表 |
| Divisible[m,n] | 检测 m 是否被 n 整除 |
| CoprimeQ[n1,n2,…] | 检测 ni 是否成对互质 |
| GCD[n1,n2,…] | n1, n2, … 的最大公约数 |
| LCM[n1,n2,…] | n1, n2, … 的最小公倍数 |
| KroneckerDelta[n1,n2,…] | 如果所有的 ni 都相等,那么 Kronecker delta |
| IntegerDigits[n,b] | b 进制下 n 的位数 |
| IntegerExponent[n,b] | 整除 n 的 b 次幂的最大值 |
Mod 也可用于实数:
由 Mod 得到的结果,其符号与第二个自变量的符号相同:
| Mod[k,n] | 结果在 0 到 n-1 之间 |
| Mod[k,n,1] | 结果在 1 到 n 之间 |
| Mod[k,n,-n/2] | 结果在 ⌈-n/2⌉ 到 ⌊+n/2⌋ 之间 |
| Mod[k,n,d] | 结果在 d 到 d+n-1 之间 |
特别当使用 Mod 来获得部分对象的索引时,指定一个偏心距常常是方便的.
| FactorInteger[n] | n 的素因子和相应指数的列表 |
| Divisors[n] | 整除 n 的整数列表 |
| Prime[k] | 第 k 个素数 |
| PrimePi[x] | 第 k 个素数 |
| PrimeQ[n] | |
| PrimeNu[n] | n 中不同素数 |
| PrimeOmega[n] | 计算关于 n 的重数(multiplicities) |
| LiouvilleLambda[n] | Liouville 函数 |
| MangoldtLambda[n] | von Mandgoldt 函数 |
| FactorInteger[n,GaussianIntegers->True] | |
高斯整数 n 的高斯素数因子和相应指数的列表 | |
| PrimeQ[n,GaussianIntegers->True] | |
应该认识到,按照现代数学的观点,整数因子分解是本质上困难的计算问题. 因此,用户能容易地输入一个整数,而 Wolfram 语言对其分解因子可能要花费天文数字长度的时间. 只要用户给出的整数位数小于 50,FactorInteger 将不会有任何困难. 然而,在一些特殊情况下,它能处理长得多的整数.
默认情况下,FactorInteger 只允许实整数. 但通过设置选项 GaussianIntegers->True,它也能处理高斯整数,即实部和虚部均为整数的复数. 正如它能唯一地分解出实素数一样,它也能唯一地分解出高斯素数. 然而,在高斯素数的选择中有一些潜在的二义性. 在 Wolfram 语言中,除了初始的 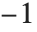 和
和  以外,因子总是被选为正实部和非负虚部.
以外,因子总是被选为正实部和非负虚部.
| PowerMod[a,b,n] | ab 模 n |
| DirichletCharacter[k,j,n] | 狄雷克莱特征 |
| EulerPhi[n] | 欧拉 totient 函数 |
| MoebiusMu[n] | 莫比乌斯函数 |
| DivisorSigma[k,n] | 除数函数 |
| DivisorSum[n,form] | 对于所有整除 n 的 i,form[i] 的和 |
| DivisorSum[n,form,cond] | 仅包含对 cond[i] 给出 True 的约数的和 |
| JacobiSymbol[n,m] | 雅可比符号 |
| ExtendedGCD[n1,n2,…] | n1, n2, … 的扩展最大公约数 |
| MultiplicativeOrder[k,n] | k 模 n 的多重阶 |
| MultiplicativeOrder[k,n,{r1,r2,…}] | 带有余数 ri 的广义多重阶 |
| CarmichaelLambda[n] | 卡米切尔函数 |
| PrimitiveRoot[n] | n 的一个原根 |
用户可以使用 PowerMod 不仅能求出正模幂,也能求出模逆. 对于负数 b,PowerMod[a,b,n] 给出,如果可能的话,一个整数 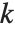 使得
使得 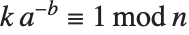 . (当这样的整数存在时,它是唯一的模 n). 如果不存在这样的整数
. (当这样的整数存在时,它是唯一的模 n). 如果不存在这样的整数 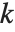 ,Wolfram 语言就使得 PowerMod 不再计算.
,Wolfram 语言就使得 PowerMod 不再计算.
DirichletCharacter 适用于很大的数:
莫比乌斯函数 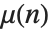 被定义为:当
被定义为:当 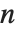 为
为 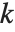 个不同素数的积时,等于
个不同素数的积时,等于 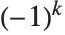 ,当
,当 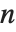 包含素数的平方(不为1)时,等于
包含素数的平方(不为1)时,等于  . 一个重要的关系是莫比乌斯逆公式,即如果
. 一个重要的关系是莫比乌斯逆公式,即如果 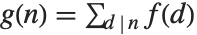 对所有
对所有 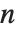 成立,那么
成立,那么 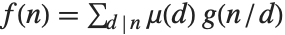 ,其中和式是对所有整除
,其中和式是对所有整除 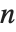 的正整数
的正整数 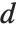 求积.
求积.
函数 DivisorSum[n,form] 表示 form[i] 的和,对于所有的除以 n 的 i. DivisorSum[n,form,cond] 仅包含对于 cond[i] 给出 True 的约数.
雅可比符号 JacobiSymbol[n,m] 当 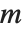 为奇数时,归结为勒让德符号
为奇数时,归结为勒让德符号  . 勒让德符号是:当
. 勒让德符号是:当 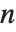 被
被 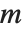 整除时,其值为零;否则,当
整除时,其值为零;否则,当 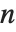 是二次余数(模素数
是二次余数(模素数 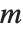 )其值为
)其值为  ,若不然其值为
,若不然其值为 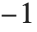 . 一个与
. 一个与 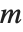 互素的整数
互素的整数 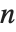 称为二次余数(模
称为二次余数(模 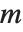 ) 是指存在一个整数
) 是指存在一个整数 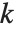 使得
使得  . 完全雅可比符号是所有满足
. 完全雅可比符号是所有满足 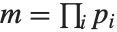 的素因子
的素因子 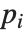 的勒让德符号
的勒让德符号  的连乘.
的连乘.
广义多重阶函数 MultiplicativeOrder[k,n,{r1,r2,…}] 给出使 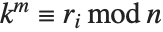 对某个
对某个 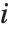 成立的最小整数
成立的最小整数 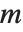 . MultiplicativeOrder[k,n,{-1,1}] 有时称作
. MultiplicativeOrder[k,n,{-1,1}] 有时称作 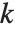 模
模 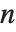 的次阶函数,记为
的次阶函数,记为 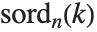 . MultiplicativeOrder[k,n,{a}] 有时被称为关于基
. MultiplicativeOrder[k,n,{a}] 有时被称为关于基 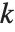 模
模 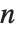 的
的 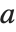 的离散对数.
的离散对数.
| ContinuedFraction[x,n] | 生成 x 的连续分式表示的前 n 项 |
| FromContinuedFraction[list] | 从其连续分式表示重构一个数 |
| Rationalize[x,dx] | 寻找 x 的有理近似,容差为 dx |
| ContinuedFraction[x] | 有理数或者二次无理数的完全连续分式表示 |
| QuadraticIrrationalQ[x] | 检测 x 是否为二次无理数 |
| RealDigits[x] | 有理数的完全数字序列 |
| RealDigits[x,b] | b 进制下的完全数字序列 |
FromDigits 重构原来的数:
| Convergents[x] | 给出 x 的有理近似的列表 |
| Convergents[x,n] | 仅给出前 n 个近似 |
| LatticeReduce[{v1v2,…}] | 整数向量 vi 的集合的规约格基 |
| HermiteDecomposition[{v1,v2,…}] | 整数向量 vi 的集合的梯阵式 |
格简化函数 LatticeReduce[{v1,v2,…}] 被使用在多种现代算术中. 基本思想是把整数向量 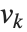 看作定义一个数学上的格. 表示格中一个点的任意向量可以被写为形如
看作定义一个数学上的格. 表示格中一个点的任意向量可以被写为形如 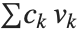 的线性组合,其中
的线性组合,其中 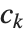 是整数. 对于一个特定的格,存在对“基向量”
是整数. 对于一个特定的格,存在对“基向量” 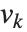 的许多可能的选择. LatticeReduce 所做的是找出对于该格的具有某种特殊性质的化简的基向量
的许多可能的选择. LatticeReduce 所做的是找出对于该格的具有某种特殊性质的化简的基向量 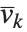 的集合.
的集合.
注意,在上一个例子中,LatticeReduce 把几乎平行的向量用更正交的向量取代. 在这个过程中,求出相当短的基向量.
对于矩阵 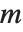 ,HermiteDecomposition 给出矩阵
,HermiteDecomposition 给出矩阵 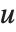 和
和 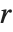 使得
使得 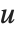 是幺模,
是幺模,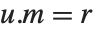 ,并且
,并且 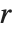 为简化行阶梯矩阵. 相对于RowReduce,枢轴(pivots)可能大于1,因为在整数环上没有分数. 枢轴(pivot)上的项通过减去枢轴同行的所有元素(pivot row)的适当的倍数来最小化.
为简化行阶梯矩阵. 相对于RowReduce,枢轴(pivots)可能大于1,因为在整数环上没有分数. 枢轴(pivot)上的项通过减去枢轴同行的所有元素(pivot row)的适当的倍数来最小化.
| DigitCount[n,b,d] | n 在 b 进制表示下的数字 d 的数目 |
| BitAnd[n1,n2,…] | 整数 ni 的位与 |
| BitOr[n1,n2,…] | 整数 ni 的位或 |
| BitXor[n1,n2,…] | 整数 ni 的位异或 |
| BitNot[n] | 整数 n 的位非 |
| BitLength[n] | 整数 n 中的二进制位数 |
| BitSet[n,k] | 在整数 n 中,设置位 k 为1 |
| BitGet[n,k] | 从整数 n 中获取位 k |
| BitClear[n,k] | 在整数 n 中,设置位 k 为0 |
| BitShiftLeft[n,k] | 向左移动整数 n,移动量为 k 位,并使用零填充 |
| BitShiftRight[n,k] | 向右移动,并且去掉最后 k 位 |
位运算作用于表示为二进制的整数. BitAnd[n1,n2,…] 产生一个整数其二进制表示的某一位为1当且仅当所有的 ni 在该位为1. BitOr[n1,n2,…] 产生一个整数其二进制表示的某一位为1,只要某个 ni 在该位为1. BitXor[n1,n2] 产生一个整数,其二进制表示的某一位为1,当且仅当 n1 或者 n2 中仅有一个在该位为1. BitXor[n1,n2,…] 的二进制表示的某一位为1,当且仅当 ni 中有奇数个在该位为1.
位运算使用在各种组合算术中. 它们也常常用于低级计算机语言中操纵位域. 然而,在这些语言中,整数有受限制的位数,典型的是8的倍数. 在 Mathematica 中的位运算实际上允许整数有不受限制的序列. 这使得 BitNot[n] 简单地等于 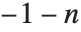 .
.
| SquareFreeQ[n] |
SquareFreeQ[n] 检查 n 是否具有平方素数因子. 这通过计算 MoebiusMu[n] 并且查看结果是否为0来实现;如果是,那么 n 包括平方素数因子,否则就不包括. 计算MoebiusMu[n] 涉及寻找 n 的最小素数因子 q. 如果 n 是一个小的素数因子(小于或者等于  ),这是很快的. 否则,用 FactorInteger 来寻找 q.
),这是很快的. 否则,用 FactorInteger 来寻找 q.
SquareFreeQ 可以处理大整数:
| NextPrime[n] | 给出大于 n 的最小素数 |
| RandomPrime[{min,max}] | 返回 min 和 max 之间的随机素数 |
| RandomPrime[max] | 返回小于或者等于 max 的随机素数 |
| RandomPrime[{min,max},n] | 返回 min 和 max 之间的 n 个随机素数 |
| RandomPrime[max,n] | 返回小于或等于 max 的 n 个随机素数 |
对于 RandomPrime[{min,max}] 和 RandomPrime[max],如果 max 是小的,则通过从素数查找表中随机选择,获取一个随机素数 p;如果 max 是大的,则通过在整数中随机搜索整数获取该随机素数. 如果在指定范围内不存在素数,则返回未计算的输入,并显示一个错误信息.
| PrimePowerQ[n] | 决定 n 是否为一个有理素数的正整数幂 |
PrimePowerQ 的算法首先计算 n 的最小素因子 p ,并且尝试除以 p 直到或者当 n 是一个素数幂的时候,得到1,或者当 n 不是一个素数幂的时候尝试除以 p 直到不可以再进行除法运算的时候.
在 GaussianIntegers 上,这是一个素数幂:
| ChineseRemainder[list1,list2] | 给出最小的非负整数 r,并满足 Mod[r,list2]==list1 |
中国剩余定理规定,一定类型的联立全等问题总是有一个解. ChineseRemainder[list1,list2] 寻找最小非负整数 r 使得 Mod[r,list2] 是 list1. 该解是唯一的 list2 的元素的最小公倍数的模.
| PrimitiveRoot[n] | 给出 n 的原根,其中 n 是素数幂或者素数幂的两倍 |
PrimitiveRoot[n]返回一个生成器,该生成器生成与 n 在模  相乘互素的数形成的集合. 这里具有一个生成器,当且仅当 n 是 2、4、一个奇素数的幂、或者一个奇素数的幂的两倍. 如果 n 是一个素数或者素数幂,将返回最小正原根.
相乘互素的数形成的集合. 这里具有一个生成器,当且仅当 n 是 2、4、一个奇素数的幂、或者一个奇素数的幂的两倍. 如果 n 是一个素数或者素数幂,将返回最小正原根.
| SquaresR[d,n] | 给出把整数 n 表示为 d 个平方数的和的表示法数目 |
| PowersRepresentations[n,k,p] | 给出把整数 n 表示为 k 个非负第 p 次整数幂的和的不同表示方法 |
| n! | 阶乘 |
| n!! | 双阶乘 |
| Binomial[n,m] | 二项式系数 |
| Multinomial[n1,n2,…] | 多项式系数 |
| CatalanNumber[n] | Catalan 数 |
| Hyperfactorial[n] | 超阶乘 |
| BarnesG[n] | Barnes G-函数 |
| Subfactorial[n] | |
| Fibonacci[n] | 斐波那契数 |
| Fibonacci[n,x] | 斐波那契多项式 |
| LucasL[n] | 卢卡斯数 |
| LucasL[n,x] | 卢卡斯多项式 |
| HarmonicNumber[n] | 调和数 |
| HarmonicNumber[n,r] | |
| BernoulliB[n] | 贝努利数 |
| BernoulliB[n,x] | 贝努利多项式 |
| NorlundB[n,a] | Nörlund 多项式 |
| NorlundB[n,a,x] | 一般贝努利多项式 |
| EulerE[n] | 欧拉数 |
| EulerE[n,x] | 欧拉多项式 |
| StirlingS1[n,m] | 第一类斯特林数 |
| StirlingS2[n,m] | 第二类斯特林数 |
| BellB[n] | 贝尔数 |
| BellB[n,x] | 贝尔多项式 |
| PartitionsP[n] | 整数 |
| IntegerPartitions[n] | 整数的划分 |
| PartitionsQ[n] | 将 |
| Signature[{i1,i2,…}] | 排列的标记 |
斐波那契数 Fibonacci[n] 满足递归关系 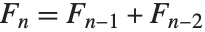 及
及 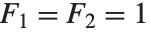 . 它们出现在离散数学问题的广泛领域中. 对于足够大的
. 它们出现在离散数学问题的广泛领域中. 对于足够大的 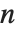 ,
,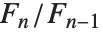 接近黄金分割. 卢卡斯数 LucasL[n] 满足与斐波那契数同样的递归关系,但是初始条件为
接近黄金分割. 卢卡斯数 LucasL[n] 满足与斐波那契数同样的递归关系,但是初始条件为  和
和 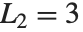 .
.
贝努利多项式 BernoulliB[n,x] 满足母函数关系 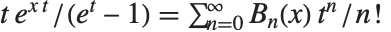 . 贝努利数 BernoulliB[n] 由
. 贝努利数 BernoulliB[n] 由 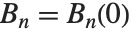 给定.
给定. 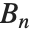 作为近似积分的欧拉——麦克劳林求和公式中项的系数出现. 贝努利数通过
作为近似积分的欧拉——麦克劳林求和公式中项的系数出现. 贝努利数通过 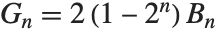 与 盖诺奇数 联系起来.
与 盖诺奇数 联系起来.
Nörlund 多项式 NorlundB[n,a] 满足母函数关系 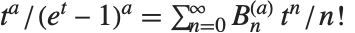 . 当
. 当  时,Nörlund 多项式给出贝努利数. 对于
时,Nörlund 多项式给出贝努利数. 对于 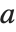 的其他正整数值,Nörlund 多项式给出高阶贝努利数. 一般贝努利多项式 NorlundB[n,a,x] 满足母函数关系
的其他正整数值,Nörlund 多项式给出高阶贝努利数. 一般贝努利多项式 NorlundB[n,a,x] 满足母函数关系 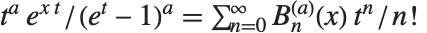 .
.
BernoulliB[n] 给出贝努利数的精确有理数结果:
斯特林数出现在许多组合枚举问题中. 对于第一类斯特林数 StirlingS1[n,m],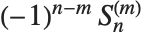 给出包含
给出包含 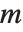 个圈的
个圈的 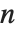 个元素的排列数目. 斯特林数满足母函数关系
个元素的排列数目. 斯特林数满足母函数关系  . 注意某些
. 注意某些 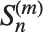 的定义与 Wolfram 语言中的不同,差别在于因子
的定义与 Wolfram 语言中的不同,差别在于因子 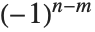 .
.
这是由 PartitionsP[4] 给出的划分数目:
标记函数 Signature[{i1,i2,…}] 给出排列的标记. 对偶排列(由偶次移项构成的)它等于 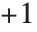 ,对奇排列它等于
,对奇排列它等于 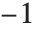 . 标记函数可以看作是完全反对称的张量,Levi‐Civita 符号 或 epsilon 符号.
. 标记函数可以看作是完全反对称的张量,Levi‐Civita 符号 或 epsilon 符号.
| ClebschGordan[{j1,m1},{j2,m2},{j,m}] | Clebsch‐Gordan 系数 |
| ThreeJSymbol[{j1,m1},{j2,m2},{j3,m3}] | Wigner 3‐j 符号 |
| SixJSymbol[{j1,j2,j3},{j4,j5,j6}] | Racah 6‐j 符号 |
Clebsch-Gordan系数和 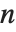 ‐j 符号出现在量子力学中的角动量中,以及循环群应用的研究中. Clebsch-Gordan系数ClebschGordan[{j1,m1},{j2,m2},{j,m}] 给出量子力学的角动量状态
‐j 符号出现在量子力学中的角动量中,以及循环群应用的研究中. Clebsch-Gordan系数ClebschGordan[{j1,m1},{j2,m2},{j,m}] 给出量子力学的角动量状态 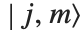 按照状态
按照状态  的乘积展开的系数.
的乘积展开的系数.
3‐j 符号 或者 Wigner 系数 ThreeJSymbol[{j1,m1},{j2,m2},{j3,m3}] 是 Clebsch–Gordan 系数的更对称的形式. 在 Wolfram 语言中,Clebsch-Gordan系数根据 3‐j 符号 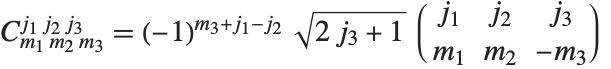 来给出.
来给出.
| Exp[z] | 指数函数 |
| Log[z] | 对数函数 |
| Log[b,z] | 对数函数 |
| Log2[z]
,
Log10[z] | 底数为 2 和 10 的对数函数 |
| Sin[z]
,
Cos[z]
,
Tan[z]
,
Csc[z]
,
Sec[z]
,
Cot[z] | |
三角函数(自变量单位是弧度) | |
| ArcSin[z]
,
ArcCos[z]
,
ArcTan[z]
,
ArcCsc[z]
,
ArcSec[z]
,
ArcCot[z] | |
反三角函数(值为弧度) | |
| ArcTan[x,y] | 自变量为 |
| Sinh[z]
,
Cosh[z]
,
Tanh[z]
,
Csch[z]
,
Sech[z]
,
Coth[z] | |
双曲函数 | |
| ArcSinh[z]
,
ArcCosh[z]
,
ArcTanh[z]
,
ArcCsch[z]
,
ArcSech[z]
,
ArcCoth[z] | |
反双曲函数 | |
| Sinc[z] | sinc 函数 |
| Haversine[z] | 半正矢函数 |
| InverseHaversine[z] | 反半正矢函数 |
| Gudermannian[z] | 古德曼函数 |
| InverseGudermannian[z] | 反古德曼函数 |
通过乘以常数 Degree 可以转化为度:
半正矢函数 Haversine[z] 被定义为 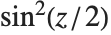 . 反半正矢函数 InverseHaversine[z] 被定义为
. 反半正矢函数 InverseHaversine[z] 被定义为 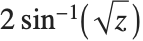 . 古德曼函数 Gudermannian[z] 被定义为
. 古德曼函数 Gudermannian[z] 被定义为  . 反古德曼函数 InverseGudermannian[z] 被定义为
. 反古德曼函数 InverseGudermannian[z] 被定义为  . 古德曼函数满足关系如
. 古德曼函数满足关系如  . sinc 函数 Sinc[z] 是一个方波信号的傅立叶变换.
. sinc 函数 Sinc[z] 是一个方波信号的傅立叶变换.
求数 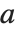 的平方根
的平方根 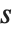 ,实际上就是求方程
,实际上就是求方程  的解. 然而,此方程一般有两个不同的解. 例如,
的解. 然而,此方程一般有两个不同的解. 例如, 和
和  都是方程
都是方程  的解. 但是当用户计算“函数”
的解. 但是当用户计算“函数”  时,通常想得到一个数. 因此必须选择其中一个. 一个标准选择是对
时,通常想得到一个数. 因此必须选择其中一个. 一个标准选择是对  ,
,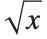 应当是正数. 这正是 Wolfram 语言函数 Sqrt[x] 所做的事情.
应当是正数. 这正是 Wolfram 语言函数 Sqrt[x] 所做的事情.
有许多数学函数,如求根,本质上给出方程的解. 对数函数和反三角函数是这样的例子. 在几乎所有的情况下,方程有许多可能的解. 但是唯一的“主要”值必须被选择. 这个选择不可能在整个复平面上都是连续的,不连续线或分支线必定出现. 这些分支线的位置常常是相当任意的. Wolfram 语言对它们进行最标准的数学选择.
| Sqrt[z] 和 z^s | |
| Exp[z] | 无 |
| Log[z] | |
三角函数 | 无 |
| ArcSin[z] 和 ArcCos[z] | |
| ArcTan[z] | |
| ArcCsc[z] 和 ArcSec[z] | |
| ArcCot[z] | |
双曲函数 | 无 |
| ArcSinh[z] | |
| ArcCosh[z] | |
| ArcTanh[z] | |
| ArcCsch[z] | |
| ArcSech[z] | |
| ArcCoth[z] |
ArcSin[z] 在分支线两边的值可能是非常不同的:
| I | |
| Infinity | |
| Pi | |
| Degree | |
| GoldenRatio | |
| E | |
| EulerGamma | 欧拉常数 |
| Catalan | Catalan 常数 |
| Khinchin | Khinchin 常数 |
| Glaisher | Glaisher 常数 |
| LegendreP[n,x] | 勒让德多项式 |
| LegendreP[n,m,x] | 相关勒让德多项式 |
| SphericalHarmonicY[l,m,θ,ϕ] | 球面调和函数 |
| GegenbauerC[n,m,x] | 盖根堡多项式 |
| ChebyshevT[n,x]
,
ChebyshevU[n,x] | 第一类和第二类切比雪夫多项式 |
| HermiteH[n,x] | 埃尔米特多项式 |
| LaguerreL[n,x] | 拉盖尔多项式 |
| LaguerreL[n,a,x] | 广义拉盖尔多项式 |
| ZernikeR[n,m,x] | 泽尼克径向多项式 |
| JacobiP[n,a,b,x] | 雅可比多项式 |
切比雪夫多项式级数常常用于函数的数值逼近. 第一类切比雪夫多项式 ChebyshevT[n,x] 由  定义. 它们被规范为
定义. 它们被规范为 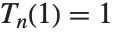 . 它们满足正交关系:当
. 它们满足正交关系:当 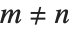 时,
时,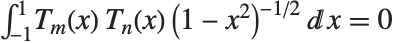 .
. 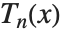 是满足相应于
是满足相应于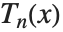 的根的
的根的 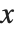 的离散点处的和式关系.
的离散点处的和式关系.
雅可比多项式 JacobiP[n,a,b,x] 出现在循环群的研究、特别是在量子力学中. 它们满足正交关系:当 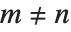 时,
时, 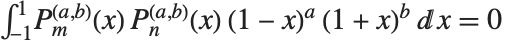 . 勒让德、盖根堡、切比雪夫和泽尼克多项式都能看作雅可比多项式的特殊情况. 雅可比多项式有时用另一种形式
. 勒让德、盖根堡、切比雪夫和泽尼克多项式都能看作雅可比多项式的特殊情况. 雅可比多项式有时用另一种形式 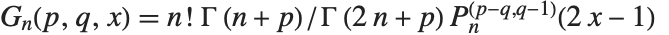 给出.
给出.
可以使用 FindRoot 求特殊函数的根:
在 Wolfram 系统中,特殊函数通常能对自变量的任意复值进行计算. 然而,在本教程中给出的定义关系常常仅适用于自变量的某些特殊选择. 在这些情况下,整个函数相应于这些定义关系的“解析延拓”. 例如,用积分式表达的函数仅当积分存在时才有效,但函数本身通常能通过解析延拓来定义.
伽马函数及相关函数
| Beta[a,b] | 欧拉贝塔函数 |
| Beta[z,a,b] | 不完全贝塔函数 |
| BetaRegularized[z,a,b] | 正则化的不完全贝塔函数 |
| Gamma[z] | 欧拉伽马函数 |
| Gamma[a,z] | 不完全伽马函数 |
| Gamma[a,z0,z1] | 广义不完全伽马函数 |
| GammaRegularized[a,z] | 正则化的不完全伽马函数 |
| InverseBetaRegularized[s,a,b] | 反贝塔函数 |
| InverseGammaRegularized[a,s] | 反伽马函数 |
| Pochhammer[a,n] | Pochhammer 符号 |
| PolyGamma[z] | 双伽玛函数 |
| PolyGamma[n,z] | 双伽玛函数 |
| LogGamma[z] | 欧拉 log-gamma 函数 |
| LogBarnesG[z] | Barnes G 函数的对数 |
| BarnesG[z] | Barnes G 函数 |
| Hyperfactorial[n] | 超阶乘函数 |
在一些运算中,特别是数论中,伽马函数的对数经常出现. 对于正实数自变量,其对数值可以通过 Log[Gamma[z]]. 轻松得到. 然而对于复自变量,该式产生伪不连续性. Wolfram 系统因此另外给出函数 LogGamma[z],它产生具有沿负实轴切割的单个分支线的伽马函数的对数.
Pochhammer 符号或上升阶乘 Pochhammer[a,n] 是 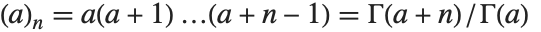 . 它常常出现在超几何函数的级数展开式中. 注意即使当其定义中出现的伽马函数为无穷大时,Pochhammer 符号也有确定的值.
. 它常常出现在超几何函数的级数展开式中. 注意即使当其定义中出现的伽马函数为无穷大时,Pochhammer 符号也有确定的值.
在某些情况下,计算不完全贝塔和伽马函数本身是不方便的,而代之以计算正则化形式,在这个形式中,用完全贝塔和伽马函数除这些函数. Wolfram 系统包含正则化的不完全贝塔函数 BetaRegularized[z,a,b],其定义为  ,且考虑奇点情况. Wolfram 系统还包含正则化的不完全伽马函数 GammaRegularized[a,z],其定义为
,且考虑奇点情况. Wolfram 系统还包含正则化的不完全伽马函数 GammaRegularized[a,z],其定义为  ,且奇点情况被考虑.
,且奇点情况被考虑.
不完全贝塔和伽马函数及其反函数在统计学中是常见的. 反贝塔函数 InverseBetaRegularized[s,a,b] 是方程  对
对 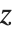 的解. 类似地,反伽马函数 InverseGammaRegularized[a,s] 是方程
的解. 类似地,反伽马函数 InverseGammaRegularized[a,s] 是方程 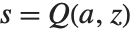 对
对 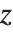 的解.
的解.
伽马函数的导数常出现在有理级数的求和当中. 双伽玛函数 PolyGamma[z] 是伽马函数的对数的导数,由 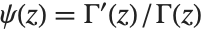 给出. 对整数自变量,双伽玛函数满足关系
给出. 对整数自变量,双伽玛函数满足关系 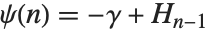 ,其中
,其中 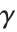 是欧拉常数 (在 Wolfram 系统中为 EulerGamma),
是欧拉常数 (在 Wolfram 系统中为 EulerGamma),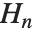 是调和数.
是调和数.
多伽马函数 PolyGamma[n,z] 由 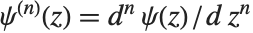 给出. 注意双伽玛函数对应于
给出. 注意双伽玛函数对应于 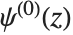 . 一般形式
. 一般形式 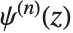 是
是  阶伽马函数的对数的导数,而非
阶伽马函数的对数的导数,而非 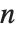 阶. 多伽马函数满足关系
阶. 多伽马函数满足关系 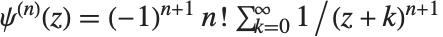 . PolyGamma[ν,z] 由任意复数
. PolyGamma[ν,z] 由任意复数 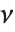 通过分数阶微积分解析延拓得到.
通过分数阶微积分解析延拓得到.
BarnesG[z] 是 Gamma 函数的推广,由泛函恒等式 BarnesG[z+1]=Gamma[z] BarnesG[z] 定义, 其中对于正数 z,BarnesG 的对数的三阶导数是正数. BarnesG 是复平面上的一个整函数.
Zeta 函数及相关函数
| DirichletL[k,j,s] | Dirichlet L-函数 |
| LerchPhi[z,s,a] | Lerch 超越函数 |
| PolyLog[n,z] | 多对数函数 |
| PolyLog[n,p,z] | 尼尔森广义多对数函数 |
| RamanujanTau[n] | Ramanujan |
| RamanujanTauL[n] | Ramanujan |
| RamanujanTauTheta[n] | Ramanujan |
| RamanujanTauZ[n] | Ramanujan |
| RiemannSiegelTheta[t] | 黎曼–西格尔函数 |
| RiemannSiegelZ[t] | 黎曼–西格尔函数 |
| StieltjesGamma[n] | 斯蒂尔吉斯常数 |
| Zeta[s] | 黎曼 ζ 函数 |
| Zeta[s,a] | 广义黎曼 ζ 函数 |
| HurwitzZeta[s,a] | Hurwitz ζ 函数 |
| HurwitzLerchPhi[z,s,a] | Hurwitz–Lerch 超越函数 |
在研究 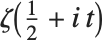 时,按照
时,按照 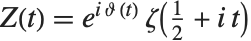 和
和 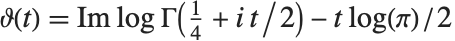 (
(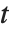 为实数)定义两个黎曼–西格尔函数 RiemannSiegelZ[t] 和 RiemannSiegelTheta[t] 往往带来方便. 注意黎曼–西格尔函数当
为实数)定义两个黎曼–西格尔函数 RiemannSiegelZ[t] 和 RiemannSiegelTheta[t] 往往带来方便. 注意黎曼–西格尔函数当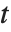 为实数时,都取实值.
为实数时,都取实值.
Ramanujan  Dirichlet L-函数 RamanujanTauL[s] 由 L(s)
Dirichlet L-函数 RamanujanTauL[s] 由 L(s)
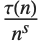 (
(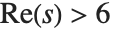 ) 定义,其系数为 RamanujanTau[n]. 与黎曼 ζ 函数类似,定义两个函数 RamanujanTauZ[t] 和 RamanujanTauTheta[t] 也会带来方便.
) 定义,其系数为 RamanujanTau[n]. 与黎曼 ζ 函数类似,定义两个函数 RamanujanTauZ[t] 和 RamanujanTauTheta[t] 也会带来方便.
多对数函数 PolyLog[n,z] 由  给出. 多对数函数有时称为 Jonquière 函数. 双对数函数PolyLog[2,z] 满足
给出. 多对数函数有时称为 Jonquière 函数. 双对数函数PolyLog[2,z] 满足 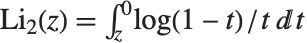 .
. 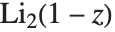 有时称为 Spence 积分. 尼尔森广义多对数函数或称超对数 PolyLog[n,p,z] 由
有时称为 Spence 积分. 尼尔森广义多对数函数或称超对数 PolyLog[n,p,z] 由 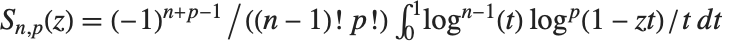 给出. 多对数函数出现在基本粒子物理学或代数 K‐理论的 Feynman 图积分中.
给出. 多对数函数出现在基本粒子物理学或代数 K‐理论的 Feynman 图积分中.
Lerch 超越函数 LerchPhi[z,s,a] 是 ζ 和多对数函数的推广,由 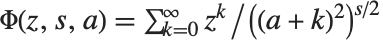 定义,其中
定义,其中 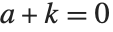 的项被排除. 许多倒数幂的和式能用 Lerch 超越函数来表示. 例如 Catalan 贝塔函数
的项被排除. 许多倒数幂的和式能用 Lerch 超越函数来表示. 例如 Catalan 贝塔函数 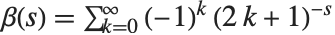 可由
可由 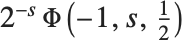 来得到.
来得到.
Lerch 超越函数也能用来计算数论中的 Dirichlet L‐级数. 基本的 L‐级数的形式为 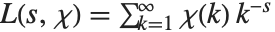 ,其中"字符"
,其中"字符" 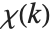 是周期为
是周期为 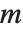 的整数函数. 这种 L‐级数可以写成 Lerch 函数的和,其中
的整数函数. 这种 L‐级数可以写成 Lerch 函数的和,其中 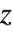 是
是  的幂.
的幂.
指数积分及相关函数
| CosIntegral[z] | 余弦积分函数 |
| CoshIntegral[z] | 双曲余弦积分函数 |
| ExpIntegralE[n,z] | 指数积分 En(z) |
| ExpIntegralEi[z] | 指数积分 |
| LogIntegral[z] | 对数积分 |
| SinIntegral[z] | 正弦积分函数 |
| SinhIntegral[z] | 双曲正弦积分函数 |
对数积分函数 LogIntegral[z] 由 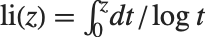 (
( )定义,并取积分的主值.
)定义,并取积分的主值.  是数论中系数分布研究的核心. 对数积分函数有时也表示为
是数论中系数分布研究的核心. 对数积分函数有时也表示为  . 在数论的某些应用中,
. 在数论的某些应用中, 被定义为
被定义为 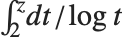 ,且不取主值. 这一定义与 Wolfram 系统中使用的定义相差常数
,且不取主值. 这一定义与 Wolfram 系统中使用的定义相差常数  .
.
正弦和余弦积分函数 SinIntegral[z] 和 CosIntegral[z] 由  和
和 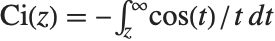 定义. 双曲正弦和余弦积分函数 SinhIntegral[z] 和 CoshIntegral[z] 由
定义. 双曲正弦和余弦积分函数 SinhIntegral[z] 和 CoshIntegral[z] 由  和
和 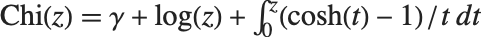 定义.
定义.
误差函数及相关函数
| Erf[z] | 误差函数 |
| Erf[z0,z1] | 广义误差函数 |
| Erfc[z] | 余误差函数 |
| Erfi[z] | 虚数误差函数 |
| FresnelC[z] | 费涅尔积分 C(z) |
| FresnelS[z] | 费涅尔积分 |
| InverseErf[s] | 反误差函数 |
| InverseErfc[s] | 反余误差函数 |
误差函数 Erf[z] 是高斯分布的积分,由 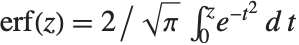 给出. 余误差函数 Erfc[z] 由
给出. 余误差函数 Erfc[z] 由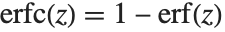 简单地给出. 虚数误差函数 Erfi[z] 由
简单地给出. 虚数误差函数 Erfi[z] 由  给出. 广义误差函数 Erf[z0,z1] 由积分
给出. 广义误差函数 Erf[z0,z1] 由积分 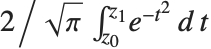 定义. 误差函数在统计学的许多计算中是很重要的.
定义. 误差函数在统计学的许多计算中是很重要的.
贝塞尔及相关函数
| AiryAi[z] 和 AiryBi[z] | Airy 函数 |
| AiryAiPrime[z] 和 AiryBiPrime[z] | Airy 函数的导数 |
| BesselJ[n,z] 和 BesselY[n,z] | 贝塞尔函数 |
| BesselI[n,z] 和 BesselK[n,z] | 修正贝塞尔函数 |
| KelvinBer[n,z] 和 KelvinBei[n,z] | 开尔文函数 |
| KelvinKer[n,z] 和 KelvinKei[n,z] | 开尔文函数 |
| HankelH1[n,z] 和 HankelH2[n,z] | 汉克尔函数 |
| SphericalBesselJ[n,z] 和 SphericalBesselY[n,z] | |
球贝塞尔函数 | |
| SphericalHankelH1[n,z] 和 SphericalHankelH2[n,z] | |
球汉克尔函数 | |
| StruveH[n,z] 和 StruveL[n,z] | Struve 函数 |
球贝塞尔函数 SphericalBesselJ[n,z] 和 SphericalBesselY[n,z],以及球汉克尔函数 SphericalHankelH1[n,z] 和 SphericalHankelH2[n,z] 出现在球对称波动现象的研究中. 这些函数通过 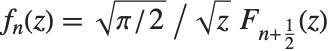 与普通函数相联系,这里
与普通函数相联系,这里 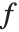 和
和 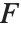 可以是
可以是 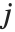 和
和  ,
, 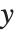 和
和 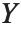 ,或者
,或者 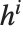 和
和 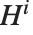 . 对于整数
. 对于整数 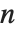 ,使用 FunctionExpand 可以将球面贝塞尔函数展开成普通函数的形式.
,使用 FunctionExpand 可以将球面贝塞尔函数展开成普通函数的形式.
特别在电子工程中,人们常常要定义开尔文函数 KelvinBer[n,z], KelvinBei[n,z], KelvinKer[n,z] 和 KelvinKei[n,z]. 这些函数通过 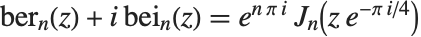 ,
, 与普通贝塞尔函数相联系.
与普通贝塞尔函数相联系.
Airy 函数 AiryAi[z] 和 AiryBi[z] 是微分方程 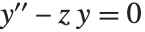 的两个独立解
的两个独立解  和
和  . 当
. 当 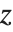 趋向于正无穷大时,
趋向于正无穷大时, 趋向于0,而
趋向于0,而  无限增大. Airy 函数与1/3整数阶修正贝塞尔函数相关. Airy 函数常作为边界值问题的解出现在电磁理论和量子力学中. 在许多情况下,也出现 Airy 函数的导数 AiryAiPrime[z] 和 AiryBiPrime[z].
无限增大. Airy 函数与1/3整数阶修正贝塞尔函数相关. Airy 函数常作为边界值问题的解出现在电磁理论和量子力学中. 在许多情况下,也出现 Airy 函数的导数 AiryAiPrime[z] 和 AiryBiPrime[z].
Struve 函数 StruveH[n,z] 出现在对整数 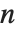 的非齐次贝赛尔方程
的非齐次贝赛尔方程 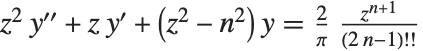 的解中. 这个方程的通解由贝塞尔函数的线性组合加 Struve 函数
的解中. 这个方程的通解由贝塞尔函数的线性组合加 Struve 函数 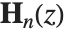 构成. 修正 Struve 函数 StruveL[n,z] 以普通 Struve 函数的形式由
构成. 修正 Struve 函数 StruveL[n,z] 以普通 Struve 函数的形式由  给出. Struve 函数特别出现在电磁理论中.
给出. Struve 函数特别出现在电磁理论中.
| BesselJZero[n,k] | 贝塞尔函数 |
| BesselJZero[n,k,x0] | 大于 |
| BesselYZero[n,k] | 贝塞尔函数 |
| BesselYZero[n,k,x0] | 大于 |
| AiryAiZero[k] | Airy 函数 |
| AiryAiZero[k,x0] | 小于 |
| AiryBiZero[k] | Airy 函数 |
| AiryBiZero[k,x0] | 小于 |
勒让德函数及相关函数
勒让德函数及缔合勒让德函数满足微分方程 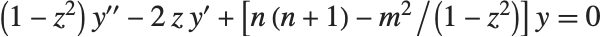 . 第一类勒让德函数, LegendreP[n,z] 和 LegendreP[n,m,z],当
. 第一类勒让德函数, LegendreP[n,z] 和 LegendreP[n,m,z],当 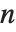 和
和 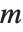 为整数时,化为勒让德多项式. 第二类勒让德函数LegendreQ[n,z] 和 LegendreQ[n,m,z] 给出微分方程的第二个线性无关解. 对于整数
为整数时,化为勒让德多项式. 第二类勒让德函数LegendreQ[n,z] 和 LegendreQ[n,m,z] 给出微分方程的第二个线性无关解. 对于整数 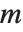 ,它们在
,它们在  处有对数奇点.
处有对数奇点. 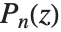 和
和 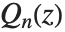 给出微分方程在
给出微分方程在  时的解.
时的解.
| LegendreP[n,m,z] 或 LegendreP[n,m,1,z] | |
包含 | |
| LegendreP[n,m,2,z] |
包含 |
| LegendreP[n,m,3,z] | 包含 |
勒让德函数的类型. 对 LegendreQ 存在类似的类型.
用同样的方法,在 GegenbauerC 等等的函数中,指标变量取任意复数就能得到盖根堡函数、切比雪夫函数、厄米函数、雅可比函数和拉盖尔函数. 然而不同于缔合勒让德函数,不需要区分这些函数的不同类型.
超几何函数及其推广
| Hypergeometric0F1[a,z] | 超几何函数 |
| Hypergeometric0F1Regularized[a,z] | 正则化超几何函数 |
| Hypergeometric1F1[a,b,z] | 库默尔合流超几何函数 |
| Hypergeometric1F1Regularized[a,b,z] | 正则化合流超几何函数 |
| HypergeometricU[a,b,z] | 合流超几何函数 |
| WhittakerM[k,m,z] and WhittakerW[k,m,z] | |
惠特克函数 | |
| ParabolicCylinderD[ν,z] | 抛物柱面函数 |
| CoulombF[l,η,ρ] | 规则库伦波函数 |
| CoulombG[l,η,ρ] | 不规则库伦波函数 |
但目前为止,我们所讨论的特殊函数多数都能被看作合流超几何函数 Hypergeometric1F1[a,b,z] 的特殊情形.
惠特克函数 WhittakerM[k,m,z] 和 WhittakerW[k,m,z] 给出正态化的库默尔微分方程(或称为惠特克微分方程)的一对解. 惠特克函数 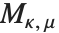 通过
通过 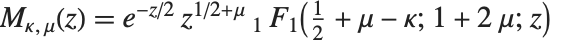 与
与 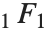 相关. 第二个惠特克函数
相关. 第二个惠特克函数 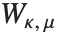 服从同一关系,只要由
服从同一关系,只要由 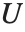 代替
代替 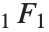 .
.
库伦波函数 CoulombF[l,η,ρ] 和 CoulombG[l,η,ρ] 也是合流超几何函数的特殊情形. 库伦波函数给出点核的库伦势中的径向薛定谔方程的解. 正则库伦波函数由 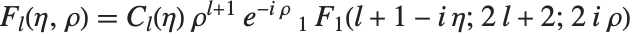 给出,其中
给出,其中 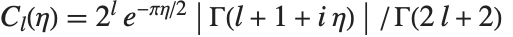 . 不规则 Coulomb 波函数
. 不规则 Coulomb 波函数 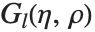 由类似的表达式给出,但用
由类似的表达式给出,但用 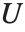 替换
替换 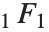 .
.
| Hypergeometric2F1[a,b,c,z] | 超几何函数 |
| Hypergeometric2F1Regularized[a,b,c,z] | |
正则化的超几何函数 | |
| HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z] | |
广义超几何函数 | |
| HypergeometricPFQRegularized[{a1,…,ap},{b1,…,bq},z] | |
正则化的广义超几何函数 | |
| MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z] | |
梅杰 G-函数 | |
| AppellF1[a,b1,b2,c,x,y] | 阿佩尔双变量超几何函数 |
梅杰 G-函数 MeijerG[{{a1,…,an},{an+1,…,ap}},{{b1,…,bm},{bm+1,…,bq}},z] 是由围道积分表示式 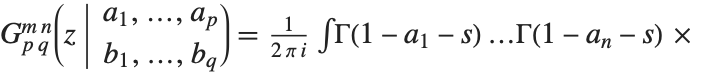
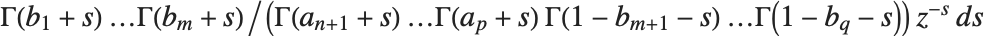 定义,其中积分的围道设在
定义,其中积分的围道设在 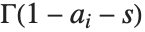 的极点和
的极点和 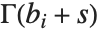 的极点之间. MeijerG 是一个非常一般的函数,它的特殊情形包括了前几节讨论的大多数函数.
的极点之间. MeijerG 是一个非常一般的函数,它的特殊情形包括了前几节讨论的大多数函数.
q 级数及相关函数
| QPochhammer[z,q] | |
| QPochhammer[z,q,n] | |
| QFactorial[z,q] | 阶乘的 |
| QBinomial[n,m,q] | 二项式系数的 |
| QGamma[z,q] | 欧拉伽马函数 |
| QPolyGamma[z,q] | |
| QPolyGamma[n,z,q] | |
| QHypergeometricPFQ[{a1,…,ap},{b1,…,bq},q,z] | |
基本超几何级数 | |
有限 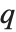 Pochhammer 符号
Pochhammer 符号 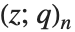 定义为乘积
定义为乘积  . 其极限
. 其极限  定义了当
定义了当  <1 时的
<1 时的 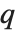 Pochhammer 符号
Pochhammer 符号 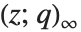 .
. 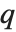 Pochhammer 符号
Pochhammer 符号 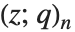 是 Pochhammer
是 Pochhammer 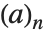 符号的
符号的 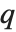 形式. 其在极限
形式. 其在极限 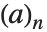
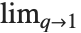
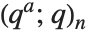 /(1-q)n 中被复原.
/(1-q)n 中被复原.
乘积对数函数
| ProductLog[z] | 乘积对数函数 |
球体函数
| SpheroidalS1[n,m,γ,z] 和 SpheroidalS2[n,m,γ,z] | |
径向球体函数 | |
| SpheroidalS1Prime[n,m,γ,z] 和 SpheroidalS2Prime[n,m,γ,z] | |
径向球体函数关于 z 的导数 | |
| SpheroidalPS[n,m,γ,z] 和 SpheroidalQS[n,m,γ,z] | |
角球体函数 | |
| SpheroidalPSPrime[n,m,γ,z] 和 SpheroidalQSPrime[n,m,γ,z] | |
角球体函数关于 z 的导数 | |
| SpheroidalEigenvalue[n,m,γ] | n 阶 m 次的球面特征值 |
径向球体函数 SpheroidalS1[n,m,γ,z] 及 SpheroidalS2[n,m,γ,z] 和角球体函数 SpheroidalPS[n,m,γ,z] 和 SpheroidalQS[n,m,γ,z] 出现在球形区域上波动方程的解中. 这两类函数均为方程 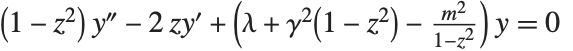 的解. 仅当
的解. 仅当  是由 SpheroidalEigenvalue[n,m,γ] 给出的球面特征值时,该方程有可规范化的解. 球体函数也可作为特征函数出现在对傅立叶变换的有限模拟中.
是由 SpheroidalEigenvalue[n,m,γ] 给出的球面特征值时,该方程有可规范化的解. 球体函数也可作为特征函数出现在对傅立叶变换的有限模拟中.
SpheroidalS1 和 SpheroidalS2 是球面贝塞耳函数  和
和  的有效球体对照,而 SpheroidalPS 和SpheroidalQS 则有效对照着勒让德函数
的有效球体对照,而 SpheroidalPS 和SpheroidalQS 则有效对照着勒让德函数 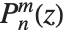 和
和 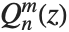 .
.  对应着长球面几何,而
对应着长球面几何,而 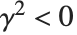 对应着扁球面几何.
对应着扁球面几何.
■ 振幅 |
■ 自变量 |
■ δ 振幅 |
■ 坐标 |
■ 特征数 |
■ 参数 |
■ 互补参数 |
■ 模 |
■ 模角 |
■ Nome |
■ 不变量 |
■ 半周期 |
■ 周期比 |
■ 判别式 |
■ 曲线 |
■ 坐标 |
| JacobiAmplitude[u,m] | 给出对应于自变量 u 和参数 m 的振幅 ϕ |
| EllipticNomeQ[m] | 给出对应于参数 m 的 nome q |
| InverseEllipticNomeQ[q] | 给出对应于 nome q 的参数 m |
| WeierstrassInvariants[{ω,ω′}] | 给出对应于半周期 {ω,ω′} 的不变量 {g2,g3} |
| WeierstrassHalfPeriods[{g2,g3}] | 给出对应于不变量 {g2,g3} 的半周期 {ω,ω′} |
椭圆积分
| EllipticK[m] | 第一类完全椭圆积分 |
| EllipticF[ϕ,m] | 第一类椭圆积分 |
| EllipticE[m] | 第二类完全椭圆积分 E(m) |
| EllipticE[ϕ,m] | 第二类椭圆积分 E(ϕm) |
| EllipticPi[n,m] | 第三类完全椭圆积分 |
| EllipticPi[n,ϕ,m] | 第三类椭圆积分 |
| JacobiZeta[ϕ,m] | 雅可比 ζ 函数 |
第一类完全椭圆积分 EllipticK[m] 由 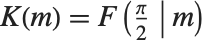 给出. 注意
给出. 注意  用来表示第一类完全椭圆积分,而
用来表示第一类完全椭圆积分,而 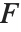 用来表示不完全的形式. 在许多应用中,参数
用来表示不完全的形式. 在许多应用中,参数 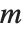 不是显式给定的,且
不是显式给定的,且  简单记作
简单记作  . 第一类互补完全椭圆积分
. 第一类互补完全椭圆积分 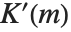 由
由  给出,常被记作
给出,常被记作  .
.  和
和 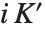 给出"实" 和 "虚" 的相应于 "椭圆函数" 中所讨论的雅可比椭圆函数的四分之一周期.
给出"实" 和 "虚" 的相应于 "椭圆函数" 中所讨论的雅可比椭圆函数的四分之一周期.
椭圆函数
| JacobiAmplitude[u,m] | 振幅函数 |
| JacobiSN[u,m]
,
JacobiCN[u,m]
, etc.
| |
雅可比椭圆函数 | |
| InverseJacobiSN[v,m]
,
InverseJacobiCN[v,m]
, etc.
| |
反雅可比椭圆函数 | |
| EllipticTheta[a,u,q] | θ 函数 |
| EllipticThetaPrime[a,u,q] | θ 函数的导数 |
| SiegelTheta[τ,s] | Siegel θ 函数 |
| SiegelTheta[v,τ,s] | Siegel θ 函数 |
| WeierstrassP[u,{g2,g3}] | Weierstrass 椭圆函数 |
| WeierstrassPPrime[u,{g2,g3}] | Weierstrass 椭圆函数的导数 |
| InverseWeierstrassP[p,{g2,g3}] | 反 Weierstrass 椭圆函数 |
| WeierstrassSigma[u,{g2,g3}] | Weierstrass σ 函数 |
| WeierstrassZeta[u,{g2,g3}] | Weierstrass ζ 函数 |
反雅可比椭圆函数 InverseJacobiSN[v,m], InverseJacobiCN[v,m] 等也是 Wolfram 语言的内置函数. 例如反函数 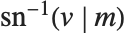 给出
给出  关于
关于 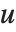 的解. 反雅可比椭圆函数与椭圆积分有关.
的解. 反雅可比椭圆函数与椭圆积分有关.
EllipticTheta[a,u,q] 中分别取 a 为 1、2、3 和 4 得到四个 θ 函数 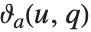 . 其定义为
. 其定义为 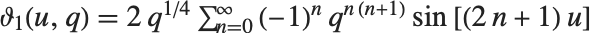 ,
, 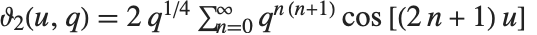 ,
,  ,
, 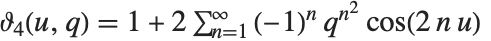 . θ 函数常写作
. θ 函数常写作  ,其参数
,其参数 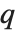 常常不写出. θ 函数有时写成
常常不写出. θ 函数有时写成 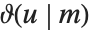 的形式,其中
的形式,其中 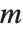 与
与 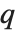 的关系为
的关系为 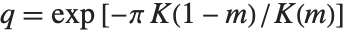 . 另外,
. 另外,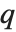 有时用
有时用  代替,两者的关系为
代替,两者的关系为 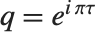 . 所有的 θ 函数满足扩散类微分方程
. 所有的 θ 函数满足扩散类微分方程 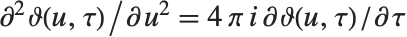 .
.
具有向量 s 的 p 维 Riemann 模块方阵(square modular matrix)的 Siegel θ 函数 SiegelTheta[τ,s] 将椭圆 θ 函数推广至复维数 p,其定义为 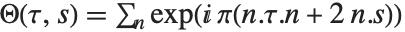 ,其中 n 跨越(runs over)全部 p 维整数向量. 特征值为 SiegelTheta[ν,τ,s] 的 Siegel θ 函数的定义由
,其中 n 跨越(runs over)全部 p 维整数向量. 特征值为 SiegelTheta[ν,τ,s] 的 Siegel θ 函数的定义由 给出,其中特征数 ν 是一对 p 维向量 {α,β}.
给出,其中特征数 ν 是一对 p 维向量 {α,β}.
Weierstrass 椭圆函数 WeierstrassP[u,{g2,g3}] 可以被看作是椭圆积分的反函数. Weierstrass 函数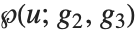 给出
给出 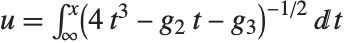 关于
关于 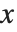 的解. 函数 WeierstrassPPrime[u,{g2,g3}] 由
的解. 函数 WeierstrassPPrime[u,{g2,g3}] 由  给出.
给出.
椭圆模函数
| DedekindEta[τ] | Dedekind η 函数 |
| KleinInvariantJ[τ] | Klein 不变模函数 |
| ModularLambda[τ] | 模 λ 函数 |
广义椭圆积分和函数
| ArithmeticGeometricMean[a,b] | |
| EllipticExp[u,{a,b}] | 与椭圆曲线 |
| EllipticLog[{x,y},{a,b}] | 与椭圆曲线 |
函数 EllipticLog[{x,y},{a,b}] 被定义为积分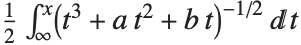 的值,其中平方根的正负通过给出使得
的值,其中平方根的正负通过给出使得 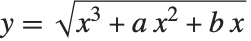 成立的
成立的 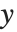 值来确定. 形如
值来确定. 形如 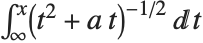 的积分可以用普通对数(和反三角函数)来表示. 可以认为 EllipticLog 给出该积分的推广,其中平方根下的多项式是三次的.
的积分可以用普通对数(和反三角函数)来表示. 可以认为 EllipticLog 给出该积分的推广,其中平方根下的多项式是三次的.
函数 EllipticExp[u,{a,b}] 是 EllipticLog 的反函数. 它返回出现在 EllipticLog 中的列表 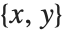 . EllipticExp 是一个椭圆函数,在复平面
. EllipticExp 是一个椭圆函数,在复平面 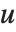 上是双周期的.
上是双周期的.
ArithmeticGeometricMean[a,b] 给出两个数 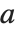 和
和 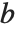 的算术-几何平均值(AGM). 该量是计算椭圆积分的和其他函数的许多数值算法的核心. 对于正实数
的算术-几何平均值(AGM). 该量是计算椭圆积分的和其他函数的许多数值算法的核心. 对于正实数 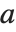 和
和 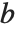 ,其 AGM 按下述方法获得:从
,其 AGM 按下述方法获得:从  ,
, 开始,然后重复变换
开始,然后重复变换 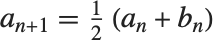 ,
,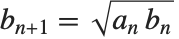 直到在要求的精度下
直到在要求的精度下  为止.
为止.
| MathieuC[a,q,z] | 具有特征值 a 和参数 q 的 Mathieu 偶函数 |
| MathieuS[b,q,z] | 具有特征值 b 和参数 q 的 Mathieu 奇函数 |
| MathieuCPrime[a,q,z] 和 MathieuSPrime[b,q,z] | Mathieu 函数的 z 导数 |
| MathieuCharacteristicA[r,q] | 具有特征指数 r 和参数 q 的 Mathieu 偶函数的特征值 ar |
| MathieuCharacteristicB[r,q] | 具有特征指数 r 和参数 q 的 Mathieu 奇函数的特征值 br |
| MathieuCharacteristicExponent[a,q] | 具有特征值 a 和参数 q 的 Mathieu 函数的特征指数 r |
Mathieu 函数 MathieuC[a,q,z] 和 MathieuS[a,q,z] 是方程  的解. 这个方程出现在涉及椭圆形状或周期位势的许多物理场合. 函数 MathieuC 定义为关于
的解. 这个方程出现在涉及椭圆形状或周期位势的许多物理场合. 函数 MathieuC 定义为关于 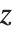 是偶函数,而 MathieuS 是奇函数.
是偶函数,而 MathieuS 是奇函数.
当  时,Mathieu 函数简化为
时,Mathieu 函数简化为  和
和 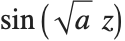 . 对于非零
. 对于非零 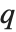 ,Mathieu 函数仅对某些
,Mathieu 函数仅对某些 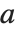 的值关于
的值关于 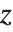 是周期的. Mathieu 特征值由 MathieuCharacteristicA[r,q] 和 MathieuCharacteristicB[r,q] 给出,其中
是周期的. Mathieu 特征值由 MathieuCharacteristicA[r,q] 和 MathieuCharacteristicB[r,q] 给出,其中 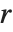 是整数或有理数. 这些值常记为
是整数或有理数. 这些值常记为 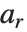 和
和 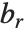 .
.
根据 Floquet 定理,任何 Mathieu 函数可以用 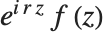 的形式写出, 其中
的形式写出, 其中  有周期
有周期 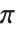 ,
, 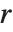 是 Mathieu 特征指数 MathieuCharacteristicExponent[a,q]. 当特征指数
是 Mathieu 特征指数 MathieuCharacteristicExponent[a,q]. 当特征指数 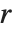 是整数或有理数时,Mathieu 函数是周期的. 然而,一般情况下, 当
是整数或有理数时,Mathieu 函数是周期的. 然而,一般情况下, 当 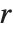 不是实整数时,
不是实整数时, 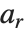 和
和 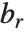 是相等的.
是相等的.
自动计算 | 指定变量的精确结果 |
| N[expr,n] | 任何精度的数值近似 |
| D[expr,x] | 导数的精确结果 |
| N[D[expr,x]] | 导数的数值近似 |
| Series[expr,{x,x0,n}] | 级数展开 |
| Integrate[expr,x] | 积分的精确结果 |
| NIntegrate[expr,x] | 积分的数值近似 |
| FindRoot[expr==0,{x,x0}] | 方程根的数值近似 |
大部分特殊方程有能用基本函数或其他特殊函数表示的导数. 但即使对导数不能明显表示的情况,也能使用 N 求出导数的数值近似值.
使用 N 给出数值近似:
| FullSimplify[expr] | 使用广泛的变换规则化简 expr |
| FunctionExpand[expr] | 展开特殊函数 |
这是的最终结果甚至不涉及 PolyGamma: